집합의 처리
상호 배타적인 여러 개의 집합을 처리해야 할 경우가 있는데 최소 신장 트리를 위한 크루스칼 알고리즘에서 상호 배타적인 집합을 처리하는 알고리즘이 필요하다.
집합의 관리에서 필요한 연산은 임의의 원소가 어느 집합에 속하는지 알나내는 연산과 두 집합을 합하는 연산이다.
여기서 말 하는 상호 배타적인 집합은 서로의 교집합이 공집합인 경우를 뜻한다.
연결 리스트를 이용한 집합의 처리
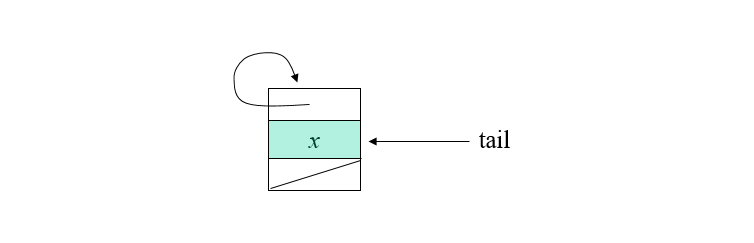
연결 리스트를 이용한 표현은 쉽고 직관적이다. ++각 원소당 하나의 노드를 만들고 이들을 연결리스트로 연결한다++
노드는 두 개의 포인터와 원소를 갖는 한 개의 필드로 이루어 진다.
다음 원소 포인터 -> 다음 원소를 가리키는 포인터. 각 집합에는 마지막 원소를 가리키는
tail이라는 변수를 둔다.
대표 원소 포인터 -> 연결 리스트의 맨 앞에 있는 원소.

)
상호 배타적 집합의 관리를 위해 필요한 ++세 가지 연산++
Make-Set(x)
- 원소 x로만 구성된 집합을 만든다.
Find-Set(x)
- 원소 x를 가진 집합을 알아낸다.
Union(x, y)
- 원소 x를 가진 집합과 원소 y를 가진 집합을 하나의 집합으로 합친다.
작업의 개요
실제적으로 연산을 해보자.

연결 리스트 집합 a와 a = {a,b,c}

연결 리스트 집합 b를 합친다고 하자! b = {d,e,f,g,h}
-
Union(a, b);Union이 이루어진다면. 대표 원소를 바꿔서 이어준다.
이렇게 행렬 a = {a,b,c}의 대표 원소를 a가 아닌 d로 연결을 시켜준다.
무게를 고려한 Union^Weighted_Union^
연결 리스트 표현에서 Make-Set은 하나의 원소로 된 집합을 초기화하는 것이므로 상수 시간이 든다. 또한 Find-Set도 상수 시간이 드는데, 이 중 상수 시간을 초과하는 것은 Union 뿐이다.
크기가 다른 두 집합이 있다고 하자.
A = {1, 3, 5}
B = {2, 4, 6, 8, 10}
Union(A, B)를 했을 때 대표 원소를 끊는 경우는 두 가지가 있다.
- A의 대표 원소를 바꾸는 경우.
- B의 대표 원소를 바꾸는 경우.
1번 같은 경우는 1, 3, 5의 움직임 (3번) , 2번 같은 경우는 2, 4, 6, 8, 10의 움직임 (5번)의 차이가 있다.
이런 방식으로 두 집합을 합치는 것을 무게를 고려한 Union이라고 한다.
수행 시간.
연결 리스트를 이용해 표현되는 배타적 집합에서 무게를 고려한 Union을 사용할 때, M번의 Make-Set, Union, Find-Set중 n번이 Make-Set이라면 이들의 총 수행 시간은?-
n번의 Make-Set을 포함하므로 원소의 총 수는 n개다.
-
Make-Set과 Find-Set은 각각 O(1)의 시간이 들고 이들을 합해도 m번을 넘지 않으므로 이들로 인한 부담은 O(m)이다.
-
결국 문제는 Union이고, Union에서 시간을 결정하는 것은 대표 노드로 포인터를 갱신하는 작업이다.
Union에서 집합에 x라는 값이 있다고 하자, 이 x값은 또한 Union함수에 의해서 만들어 졌으므로 식은
Union(n/2, n/2)이 된다. 또한 n/2도Union(n/4, n/4)로 이루어 져 점점 1 -> 2^2^ -> 2^3^ -> 2^4^ 의 비율로 커진다.
하지만 원소의 총 수는 n이므로 모든 원소를 고려한다면 기껏해야 nLog(2^n^)을 넘지 않는다. 그러므로 전체 시간은
O(m+nlogn) 이다.
트리를 이용한 집합의 처리
연결 리스트를 이용한 Union 에서는 결국 두 번의 포인터 갱신이 필요한데 이 마저도 효율적으로 할 수 있게 해주는 것이 바로 트리를 이용한 집합의 처리이다.
기본 원리
트리를 이용한다면 연결 리스트에서의 것 처럼 두 번의 갱신이 필요하지 않고 단지 루트 노드의 위치만 바꿔준다면 한 번에 Union이 가능하다.
트리를 이용하려면 두 가지의 특징을 알아야 한다.
트리의 두 가지 특징
- 자식 노드가 부모 노드를 가리킨다.
- 트리의 루트를 집합의 대표 원소로 삼는다.
직관적인 그림으로 보자.

a는 자기 자신을 가리키고 루트 노드가 된다.
c는 자기 자신을 가리키고 루트 노드가 되며 자식 노드 b와 h가 향하고 있다.
트리의 Union
트리를 이용한 표현에서 두 집합을 합치는 작업은 연결 리스트의 방법 보다 아주 간단하다.
두 집합 중 한 집합읠 ㅜ트가 다른 집합의 루트를 가리키도록 포인터 하나만 변경해준다면 끝!

하나의 원소로 구성된 집합은 노드를 하나 만들고 이 노드의 부모가 자신이 되도록 포인터를 만들어놓으면 된다.
// 부모 노드 : p[x]
// 노드 x를 유일한 원소로 하는 집합을 만든다.
Make_Set(x){
p[x] <- x;
}
// 노드 x가 속한 집합과 노드 y가 속한 집합을 합친다.
Union(x, y){
p[Find_Set(y)] <- Find_Set(x);
}
// 노드 x가 속한 집합을 알아낸다. 노드 x가 속한 트리의 루트 노드를 리턴한다.
Find_Set(x){
if(x=p[x]) then return x;
else return Find_Set(p[x])
}
연산의 효율을 높이는 방법
랭크를 이용한 Union
- 각 노드는 자신을 루트로 하는 서브트리의 높이를 Rank라는 이름으로 저장한다.
- 단 하나의 노드로 된 트리의 높이는 0이라고 정의한다.
- 루트 노드의 랭크가 해당 집합의 랭크가 된다.
경로 압축
- Find-Set을 행하는 과정에 경로의 길이를 줄이는 아이디어이다.
- 기본적으로는 Find-Set과 같이 행하되 Find-Set(x)를 수행하는 과정에서 만나는 모든 노드가 직접 루트 노드를 가리키도록 한다.
'💻 Computer Science > - Data Structure, Algorithm' 카테고리의 다른 글
| [알고리즘-PS] Java에서 선형 검색 구현하는 방법. (0) | 2020.02.12 |
|---|---|
| [알고리즘 문제 풀이 스킬] 자바에서 int형 숫자의 자릿수를 구하는 방법. feat. 백준 2577번 (0) | 2020.01.20 |
| [알고리즘-이론] 해시 테이블 (Hash Table) (0) | 2019.11.23 |
| [알고리즘-이론] 레드 블랙 트리(Red-Black Tree) (0) | 2019.11.23 |
| [알고리즘-이론] 이진 검색 트리(Binary Search Tree) (0) | 2019.11.23 |

댓글